2020年数学建模优秀论文展示（历届数学建模优秀论文）

大家好，我是小新，我来为大家解答以上问题。2020年数学建模优秀论文展示，历届数学建模优秀论文很多人还不知道，现在让我们一起来看看吧！

超声扩频测距系统数学建模

摘　要:对超声扩频测距系统的数学建模问题进行了研究。首先,利用直流-直流(DC-DC)升压模块构造了超

声换能器的发射与回声接收电路;其次,利用自回归滑动平均(ARMA)模型建立了此超声测距电路的输入-输出传

递函数,并通过实验验证了传递函数的准确性。此模型的建立可便于超声扩频测距系统对脉冲编码和调制方式的

选择,省去了繁琐的硬件验证。

关键词:超声测距系统;扩频;编码;调制;自回归滑动平均模型;传递函数

　　为解决传统脉冲回波法超声测距系统中作用

距离与测距分辨力的矛盾,近年来国内外一些学者

开始尝试扩频超声测距技术[1-11],即在超声发射端,

通过对扩频编码与调制脉冲信号的功率放大来激励

超声换能器,在接收端对超声回波信号经放大后采

用相关或匹配滤波技术进行处理获得窄脉冲从而实

现解扩。将现代雷达中的脉冲压缩技术应用到超声

测距中,既保持了窄脉冲的高测距分辨力,又获得了

宽脉冲的强检测能力。另外在多个超声换能器同时

工作的场合,合理地选择超声扩频方案还可有效地

提高信噪比,抑制噪声干扰。因此,超声扩频测距系

统中发射脉冲序列的扩频编码与调制方式的选择至

关重要,当前使用较多的是伪随机扩频技术[1-10],如

文献[1-2,4-5]采用二值m序列扩频码,其中文献

[4]中采用幅移键控(ASK)结合m序列伪随机码对

超声载波信号进行调制;文献[3]采用Gold序列结

合二值相移键控(BPSK)调制实现超声扩频;文献

[6]使用最大长度移位寄存器序列(M序列)对脉冲

进行编码。文献[11]采用混沌扩频码对脉冲的位置

进行调制,即混沌脉冲位置调制(CPPM)。文献[1]

给出了压电型超声扩频测距的硬件设计方案,其发

射端采用变压器对扩频脉冲信号进行功率放大,回

收端采用二级放大结合带通滤波实现对回声信号的

接收。

本文给出了基于直流-直流(DC-DC)升压模块

激励超声换能器的发射与回声接收电路,并推导了

超声发射至回收端的传递函数。此超声扩频测距系

统数学模型的建立可方便对超声扩频码与调制方式

的选择,免去硬件验证的繁琐。

1　超声发射与接收电路

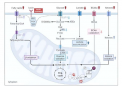
超声扩频测距系统的原理如图1所示。数字信

号处理器(DSP)给出扩频的发射脉冲序列,此序列

经DC-DC升压模块放大为200~400 V的高压脉冲

序列后激励静电超声换能器发射超声波。实验采用

的超声换能器为Polaroid 600系列静电换能器,它

被广泛用于介质为空气的测距场合。换能器的中心

图1　超声扩频测距系统原理框图

频率约在50 kHz,有效频带范围(-5 dB)在40~

70 kHz,波束角约为15°,工作时需200 V左右的直

流偏置电压。发射的超声波遇到障碍物后返回,经

自增益放大、滤波、模/数转换后,再通过相关解扩算

出渡越时间(TOF),从而获得待测量的距离。

基于DC-DC模块的超声激励与接收的硬件电

路如图2所示。其中DC-DC模块的输入电压为

5 V,输出电压在200~400 V范围内可调;图2(a

中的“扩频脉冲序列”由DSP发出;场效应管的作用

相当于一个开关,当DSP输出高电平时,场效应管

导通,换能器两端电压接近于零;当DSP输出低电

平时,场效应管截止,换能器两端电压接近DC-D

模块输出电压。图2(b)中的电容用于隔离直流分

量。

超声测距系统自回归滑动平均(ARMA)

模型的构建

2.1　超声发射与接收电路的线性特性

为采用ARMA模型建立超声电路的传递函

数,对系统的线性特性做了验证。验证的思路是分

别从DSP发射一个上升沿和一个下降沿,记录各自

的回声序列,如图3所示。

　　DSP发射单个脉冲信号如图4所示。为验证

电路的线性特性,需比较实际单个脉冲信号产生的

回声序列与上升沿和下降沿回声序列叠加的结果是

否吻合。比较结果可知,实际单个脉冲信号产生的

回声序列与上升沿和下降沿回声序列叠加的结果吻

合,从而验证了电路的线性特性。

2.2　电路传递函数的构造

(1)单个冲激信号至回声序列的传递函数

这里的单个冲激信号指的是DSP输出的单个

上升沿或下降沿。由2.1分析可知,本文给出的超

声发射和回声接收电路为线性的,所以可采用AR-

MA模型来建立系统的传递函数。系统的输入为单

个冲激信号,输出是接收的未放大的回声信号序列。

在z域下可用如图5所示来表示输入/输出关系。

建模的任务是确定分子阶数Nb和分母阶数

Na,以及系数序列ai(i=1,…,Na)和bj(j=0,1,

…,Nb)。经实验可知,阶数Nb和Na在300的情况

下,可满足要求。本文采用Prony法[12]确定分母

和分子多项式系数ai和bj。将H(z)写成冲击响应

hi的形式为

H(z)=∑

∞

n=0hiz-i(2)

结合式(1)、(2),可得

本文到此讲解完毕了，希望对大家有帮助。